Actuation

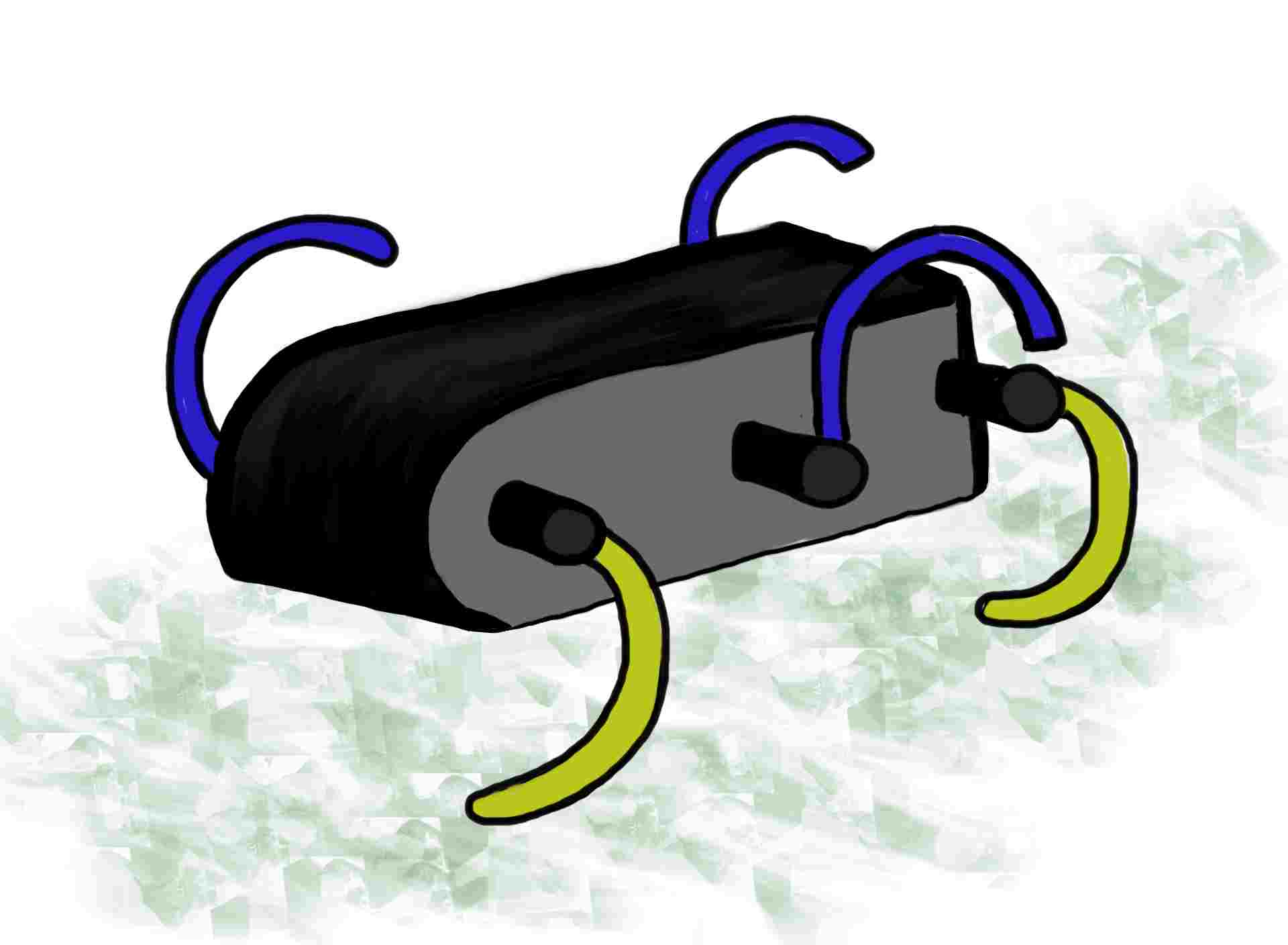
Position of the Whegs

The Whegs have to be placed in a particular fashion in order to have a smooth walking of the robot. On one side, the two external Whegs has to be in phase, and the middle one in opposition of phase. On the other side, the middle Wheg will be in phase with the two external Whegs of the opposite side of the robot, and the others with the oppisite side middle Wheg, as shown on the figure.

Number of Motors

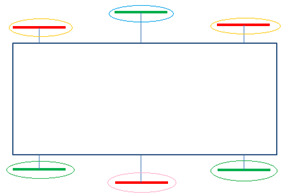
Actuation of the Whegs

Because the robot has six Whegs, two, four or six motors can be used for the actuation. When two motors are used, each of them actuates one side. This solution is the simplest one because only two control loops are needed in this case (one for each motor). Indeed, the motors that can be used in this project are servomotors with continuous rotation (therefore without position control) and DC motors (needing a H-bridge to be controlled). The remaining question is about the power of the motors: do the motors give enough torque to each actuates three Whegs?

With four motors, the motors are distributed like on the figure (one for the blue circle, one for the pink one, one for the orange ones and one for the green ones). But this configuration is much more complicated than using only 2 motors. And it seems to be unnecessary to have such a complexity.

The simplest solution (mechanically) is to use six motors, one for each Whegs. But in this case, six control loops are needed and the robot could become too expensive.

So finally, the decision is made to use two motors for the actuation of the robot. The question remaining is how to distribute the actuation from the two motors to all the Whegs. This will be discussed in the "Distribution of Actuation" section.

Maximal torque

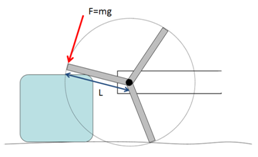
Maximal torque

To know the specifications for the motors, the largest possible torque is computed. The worst case scenario is then use to have a limiting value. In this case, there are three Whegs on the floor with a maximal torque (a perpendicular one) like on the drawing. It gives a torque which is

M=m/3×9.81×L

where L is the length of a leg and m is the mass of the robot (divided by three because there are three Whegs on the floor). The legs have a length of 7 cm and the weight of the robot is about 2 kg. So the maximal torque will be

M=2/3×9.81×0.07=0.4578 Nm

But in the worst case, a motor has to actuate at least two Whegs, so the maximal torque needed from the motor will be given by

M=2×0.4578=0.9156Nm?1Nm

But this result corresponds to the worst case scenario. Therefore, this result is probably slightly too high, and a lower value of torque can be considered.

Speed of the robot

The robot does not have to be really fast. A velocity around 1 m/s will be sufficient. With the dimension of the Whegs (0.07m), this gives a rotation speed around 120 rpm.

Choice

For the choice of the motors, specifications are not that narrow. Torque and velocity can be a little bit lower than the calculated values, the calculations gives an order of magnitude and an idea on the typical values that should be found.

Back to Top